Dividing Fractions Keep Change Flip
Complete Guide: Dividing Fractions
Key Question: How do y'all divide fractions past fractions and fractions with whole numbers?
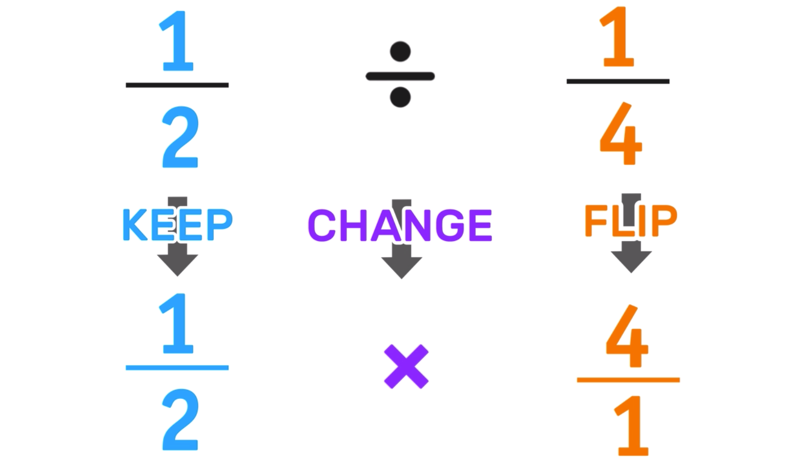
Larn to split up fractions using 3 easy steps.
Welcome to this free pace-by-step guide to dividing fractions. This guide will teach you how to apply a simple three-footstep method called Keep-Change-Flip to easily carve up fractions past fractions (and fractions by whole numbers as well).
Below you lot will observe several examples of how to divide fractions using the Continue-Change-Flip method forth with an explanation of why the method works for whatever math trouble that involves dividing fractions. Additionally, this free guide includes an animated video lesson and a complimentary practice worksheet with answers!
Are you ready to go started?
Dividing Fractions: Multiplication Review
Before you lot acquire how to divide fractions using the Keep-Change-Flip method, you need to make sure that you understand how to multiply fractions together (which is even easier than dividing!).
Since multiplying fractions is typically taught before dividing fractions, you may already know how to multiply two fractions together. If this is the case, you can skip ahead to the next section.
However, if y'all want a quick review of how to multiply fractions, here is the dominion:
Multiplying Fractions Rule: Whenever multiplying fractions together, multiply the numerators together, then multiply the denominators together equally follows…
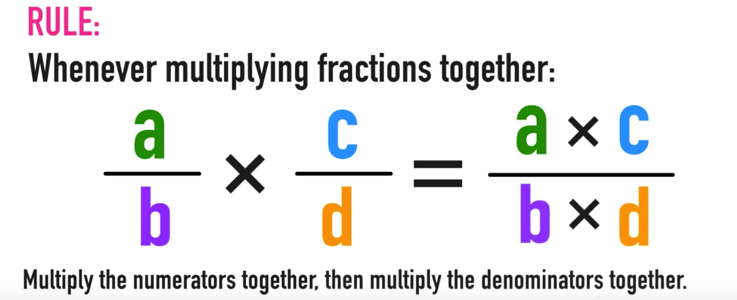
For example, three/4 x i/two tin can be solved as follows:



Dividing Fractions Examples!
Now that yous know how to multiply fractions, you are ready to learn how to dissever fractions using the simple three-step Keep-Change-Flip method.
Let's start with a simple example
Dividing Fractions Example one
Example i: What is i/2 ÷ 1/4 ?
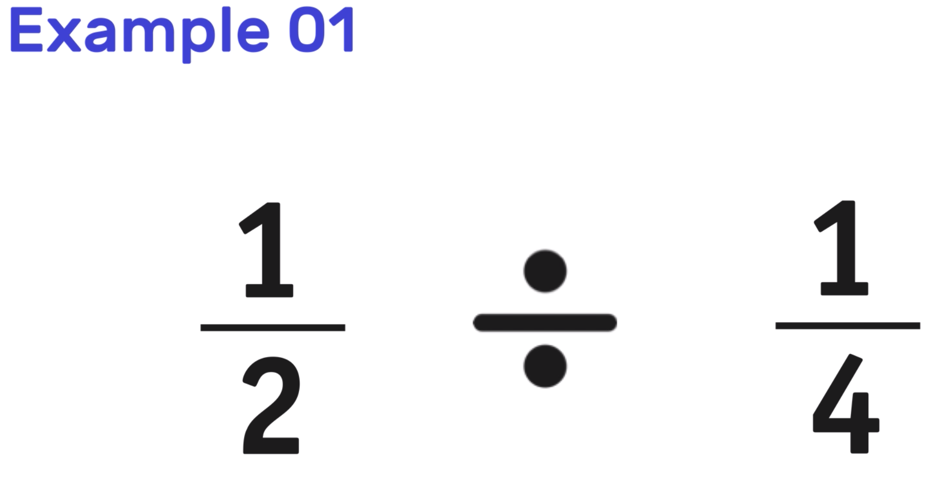
To solve this example (and any problem where you have to divide fractions, we are going to use the Keep-Change-Flip method)

Where:
1.) KEEP = Keep the first fraction equally is and merely leave it alone.
two.) CHANGE = Change the partitioning sign to a multiplication sign.
3.) FLIP = Flip the second fraction (bandy the numerator and the denominator)
These steps can be practical to case 1 every bit follows:
Again, after applying Keep-Change-Flip, we take transformed the original problem of 1/2 ÷ i/iv as follows:

At present you can solve the problem past multiplying the fractions together and simplifying if necessary:


Notice that 4/2 can be simplified.

The final answer is 2, and we tin conclude that the reply to the original trouble is…
Last Reply: 1/two ÷ 1/iv = 2

Why Does This Reply Mean?
In example 1, nosotros concluded that 1/2 ÷ 1/4 = 2. Just what does this really mean?
If we think about 1/2 ÷ one/4 in the form of a question: How many ane/4s are in 1/2?
And and so if nosotros visualize 1/4 and 1/2, we can clearly meet that there are 2 i/4s in 1/2, which is why the terminal respond is 2.
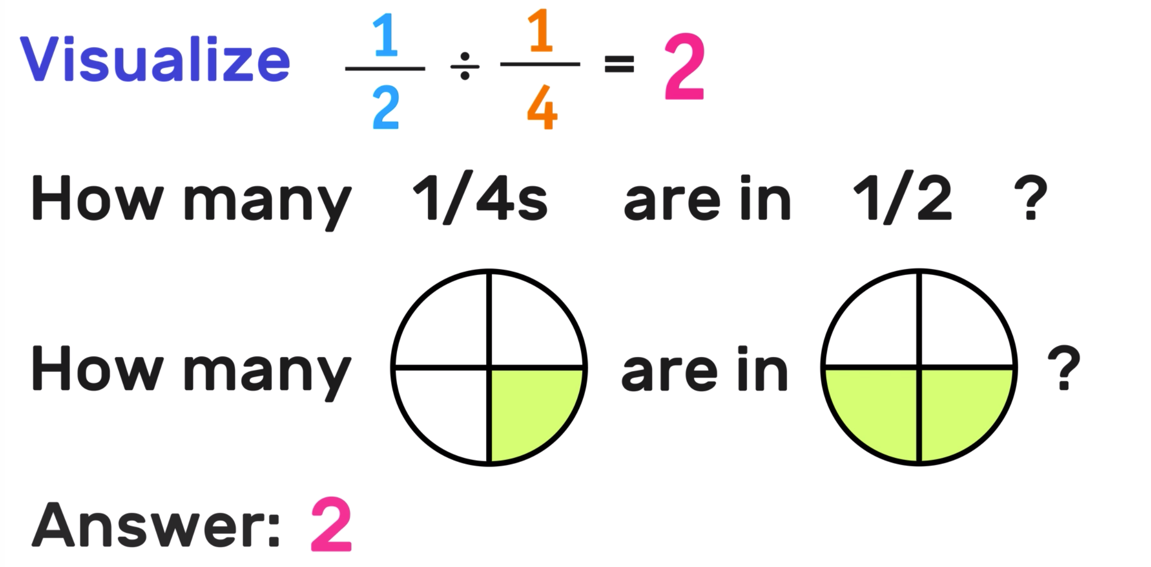
Fraction Divided by Fraction: Case 2
Example 2: What is 2/9 ÷ 1/three ?

Just similar case 01, you can solve this problem by using the keep change flip method every bit follows:
1.) Keep the first fraction ii/9 every bit is.
2.) Change the division sign to multiplication.
3.) Flip the second fraction to turn 1/3 into 3/1


Adjacent, perform 2/9 10 3/1 as follows and simplify the respond if you tin:
In this example, 6/nine is not the final answer, since it can be reduced to 2/three
The final answer is 2/iii, and we tin conclude that the answer to the original trouble is…
Final Answer: two/nine ÷ 1/3 = 2/iii

Dividing Fractions past Whole Numbers: Example 3
What if you have to split up a fraction with a whole number? Information technology turns out the procedure is exactly the aforementioned as the previous examples!
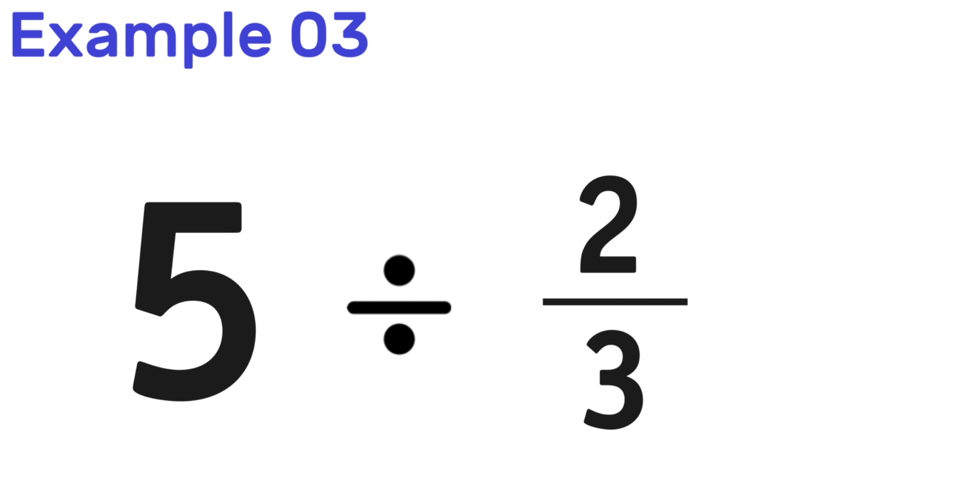
Example 03: What is 5 ÷ 2/3 ?
Detect that, in this instance, yous are dividing a fraction with a whole number. Merely it is really very easy to convert a whole number into a fraction. All that you have to do is rewrite the number as fraction where the number itself is in the numerator and the denominator is one.
For example, 5 can be rewritten as 5/one and this dominion applies for any whole number!

Now that you have rewritten the whole number every bit a fraction, you tin can use the Keep-Modify-Flip method to solve the problem.
1.) Continue the first fraction 5/1 as is.
2.) Change the division sign to multiplication.
3.) Flip the second fraction to turn ii/3 into three/2

Finally, multiply the fractions together and simplify if possible to detect the final reply as follows:


15/2 can non be simplified, still, it can exist expressed every bit vii & i/2

In this instance, the reply tin exist expressed equally 15/ii or as vii & 1/2.
And you can conclude that the reply to the original problem is…
Final Respond: 5 ÷ 2/3 = fifteen/2 or 7&1/2
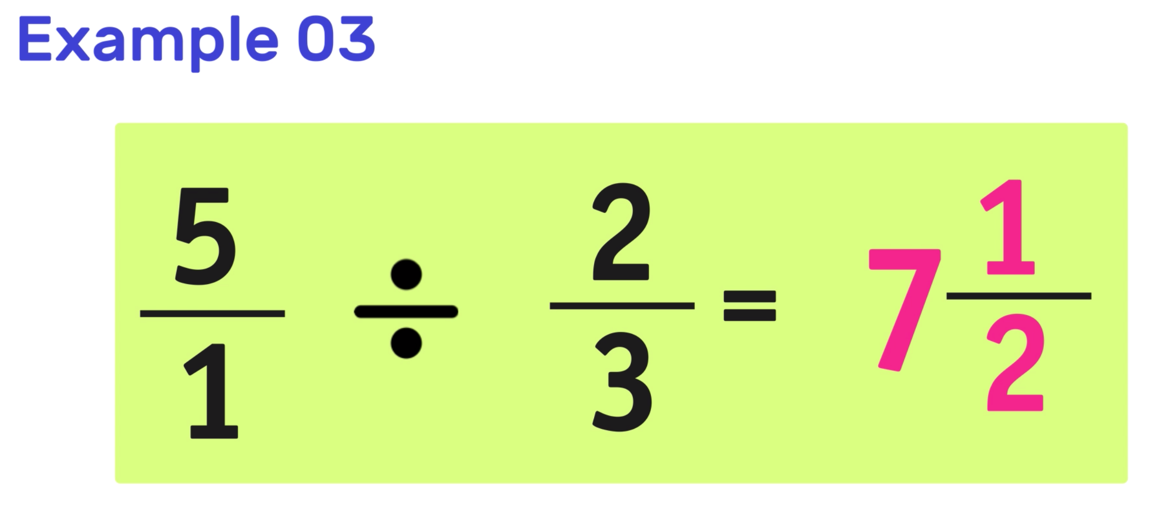
Still confused? Check out the animated video lesson below:
Video: Dividing Fractions Explained!
Check out the video lesson beneath to learn more near how to split up fractions by fractions and fractions by whole numbers:
Dividing Fractions Worksheet
Free Worksheet!
Are you looking for some actress practice dividing fractions? Click the links below to download your free worksheets and answer cardinal:
CLICK Here TO DOWNLOAD YOUR Gratuitous WORKSHEET
Tags:divide fractions, dividing fractions by whole numbers, dividing fractions examples, fraction divided by fraction
Keep Learning:
i Comment
Dividing Fractions Keep Change Flip,
Source: https://www.mashupmath.com/blog/dividing-fractions-examples
Posted by: demeryarman1949.blogspot.com




0 Response to "Dividing Fractions Keep Change Flip"
Post a Comment